RGB to YCbCr image conversion

One important task in image processing applications is the color space conversion. Real-time images and videos are stored in RGB color space, because it is based on the sensitivity of color detection cells in the human visual system. In digital image processing the YCbCr color space is often used in order to take advantage of the lower resolution capability of the human visual system for color with respect to luminosity. Thus, RGB to YCbCr conversion is widely used in image and video processing[1].

Given a digital pixel represented in RGB format, 8 bits per sample, where 0 and 255 represents the black and white color, respectively, the YCbCr components can be obtained according to equations (1) to (3):

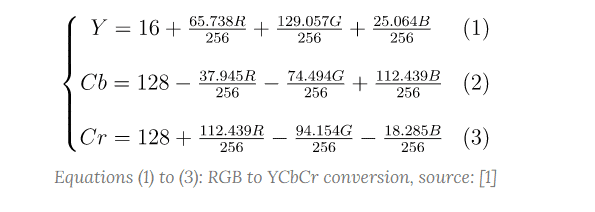
So approximating the equations to the nearest integers-

We get-

Y = 16 + (66R + 129G + 25B)/256 ...(1)

Cb = 128 - (38R - 74G + 112B)/256 ...(2)

Cr = 128 + (112R - 94G - 18B)/256 ...(3)

Though this is quite a bold approximations and we will incur quite an accuracy loss, yet we go for these because 
floating point hardwares are bulky, costly and consumes a lot power.

Again we cannot use software float libraries to solve this issue, because then we will not gain 
any hardware acceleration. Then the need for any dedicated IP for that matter is nonexistent.

So for ultra low power applications, this is okay. 


Now we know that a binary number "<<"ed by one place means multiplication of the binary number by 2^1

Similarly a binary number "<<"ed by n places means multiplication of the binary number by 2^n
And a binary number ">>"ed by n places means division of the binary number by 2^n

Therefore the above equations become-

Y = 16 + ( ((2^6*R + 2^1*R) + (2^7*G + G) + (2^4*B + 2^3*B + B)) / (2^8) ) ...(1)

Cb = 128 + ( -((2^5*R)+(2^2*R)+(2^1*R)) -((2^6*G)+(2^3*G)+(2^1*G) +((2^7*B)-(2^4*B)) ) / (2^8) ) ...(2)

Cr = 128 + ( ((2^7*R)-(2^4*R)) -((2^6*G)+(2^5*G)-(2^1*G)) -((2^4*B)+(2^1*B))  / (2^8) ) ...(3)

which is nothing but

Y = 16 + ( ((R<<6)+(R<<1)) + ((G<<7)+(G)) + ((B<<4)+(B<<3)+(B)) >> 8 ) ...(4)

Cb = 128 + ( -((R<<5)+(R<<2)+(R<<1)) -((G<<6)+(G<<3)+(G<<1)) +((B<<7)-(B<<4)) >> 8 ) ...(5)

Cr = 128 + ( ((R<<7)-(R<<4)) -((G<<6)+(G<<5)-(G<<1)) -((B<<4)+(B<<1))  >> 8 )  ...(6)

Shift operations are used because in case of synthesis from RTL to Gate level, hardware cost will be less. 
Otherwise for "*", "/", bulky multipliers and dividers would have been utilised

In this case, hardware will be nothing but a series of shift registers

Image and Video consumes a lot of data. One of the reasons is because they are represented in the RGB format. However, it is not worth to store or transmit information in this color space representaion, because it will consume large bandwidth. Thus all the pixels should be converted to YCbCr.

Let us take a pratical example to understand this-

To understand the effect of converting RGB to YCbCr, we will use the Figure (1).

Using Matlab or Octave let's do some processing on the image. Python can also be used. For example, the code below reads the image file "rgb.png":

// Matlab code to read an image
// RGB to YCbCr with Matlab
I = imread('rgb.png');
figure(1), imshow(I);

A color image has three channels (red, green and blue components). To access each component of the image, the Matlab code below can be used:

//Matlab code to access each channel of the image
// RGB to YCbCr with Matlab
R = I(:,:,1);
G = I(:,:,2); 
B = I(:,:,3); 
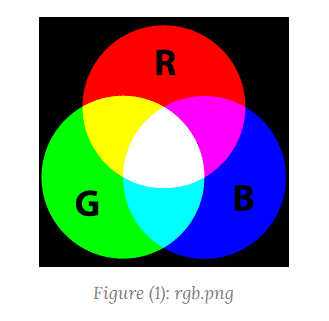
figure(2), imshow(R), figure(3),imshow(G),figure(4), imshow(B);

Each component of the image can be seen in Figures (2) to (4). Note that each channel has only the corresponding color.

The Matlab provides the function rgb2ycbcr that converts an image from RGB to YCbCr.

The script to convert the image from one space to another and to access each component (Y, Cb and Cr) can be seen below:

// Matlab code to convert from RGB to YCbCr and to access each channel of the converted image
// RGB to YCbCr with Matlab
I2 = rgb2ycbcr(I);
Y = I2(:,:,1); 
Cb = I2(:,:,2); 
Cr = I2(:,:,3); 
figure(5),imshow(I2), figure(6), imshow(Y), figure(7), imshow(Cb),figure(8), imshow(Cb);

The converted image in the YCbCr space can be seen in Figure (5).

It has three components: the luminance Y, the blue difference Cb and the red difference Cr.

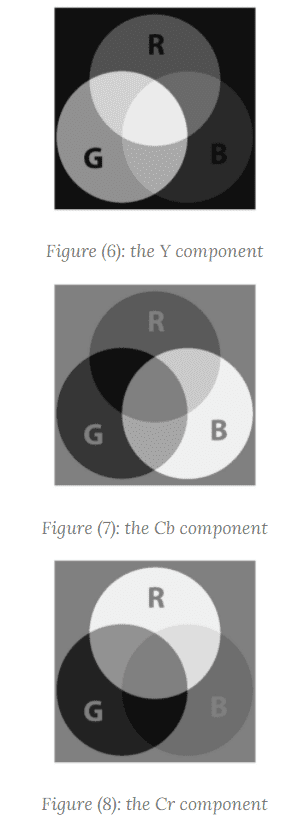
The Y component only filters the luminance (brightness) of the image (see Figure (6)); the Cb and Cr components subtract the red and blue colors, respectively, from the image (see Figures (7) and (8)).

Hardware implementation

The hardware implementation of the RGB to YCbCr converter may be done using equations (4) to (6).

The computation is done using only shift registers and adders. Each component is described in Figures (9) to (11).

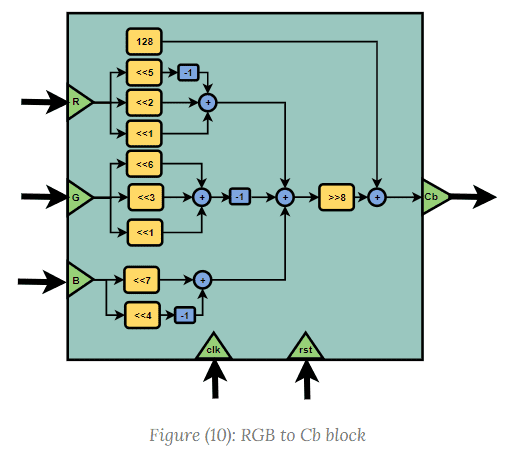
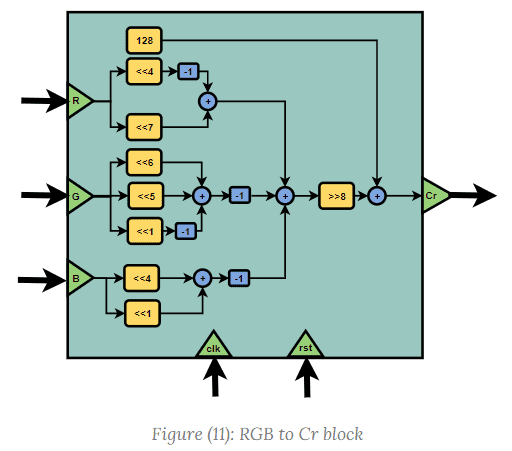
The module of the converter has two interfaces:

• The input RGB interface rgb_if: contains the three components of the RGB pixel, plus the clock and reset signals
• The output YCbCr interface ycbcr_if: contains the three components of the YCbCr pixel, plus the clock and reset signals

//SystemVerilog code of the RGB interface (rgb_if.sv)

interface rgb_if(input logic clk, rst);
    logic [7:0] R, G, B;
    
    modport in(input clk, rst, R, G, B);
endinterface : rgb_if

//SystemVerilog code of the YCbCr interface (ycbcr_if.sv)

interface ycbcr_if(input clk, rst);
    logic [7:0] Y, Cb, Cr;
    
    modport out(input clk, rst, output Y, Cb, Cr);
endinterface : ycbcr_if

The SystemVerilog implementation of the RGB_2_YCbCr converter can be seen below:

//main converter module

module RGB_2_YCbCr(rgb_if.in in, ycbcr_if.out out);

   always @(posedge in.clk)begin
       if(in.rst) begin
          out.Y <= 0;
          out.Cb <= 0;
          out.Cr <= 0;
       end
       else begin
          out.Y <= 16+(((in.R<<6)+(in.R<<1)+(in.G<<7)+in.G+(in.B<<4)+(in.B<<3)+in.B)>>8);
          out.Cb <= 128 + ((-((in.R<<5)+(in.R<<2)+(in.R<<1))-((in.G<<6)+(in.G<<3)+(in.G<<1))+(in.B<<7)-(in.B<<4))>>8);
          out.Cr <= 128 + (((in.R<<7)-(in.R<<4)-((in.G<<6)+(in.G<<5)-(in.G<<1))-((in.B<<4)+(in.B<<1)))>>8);
       end
    end
endmodule : RGB_2_YCbCr

The SystemVerilog implementation of the testbench of the RGB_2_YCbCr is shown below.

The ROM provides the pixels to stimulate the RGB_2_YCbCr module.

//ROM giving RGB inputs

module ROM(input logic [2:0]address, //2^3 = 8 addresses in ROM 
           output logic [23:0]data);
   
   always_comb begin
     case (address)
       00: data <= 0;
       01: data <= (123<<16)+(88<<8)+60;
       02: data <= (100<<16)+(200<<8)+110;
       03: data <= (50<<16)+(50<<8)+10;
       04: data <= (251<<16)+(135<<8)+160;
       05: data <= (185<<16)+(69<<8)+45;
       06: data <= (196<<16)+(188<<8)+201;
       07: data <= (132<<16)+(168<<8)+74;
     endcase
   end
endmodule : ROM

//Testbench
`ifndef TB
`define TB


parameter N_ADDR = 8;


module top;
  logic clk;
  logic rst;
  logic [2:0] addr;
  logic [23:0] data;
  int i;
  

  //Instantiation
  rgb_if in(clk, rst);
  ycbcr_if out(clk, rst);
  RGB_2_YCbCr rtl(in, out); //interfaces are taken as parameters to module
  ROM image(.address(addr), .data(data));
  

  //clock generation
  always #5 clk = ~clk;


  initial begin
    clk = 0;
    rst = 1;
    $display("Reset started @%0t", $time);
    #22 rst = 0;
    $display("Reset ended @%0t", $time);
     
    for(i = 0; i <= N_ADDR; i++)begin
      @(posedge clk);
      addr <= i;
      in.R <= data[23:16];
      in.G <= data[15:8];
      in.B <= data[7:0];
      $display("R = %d G = %d B = %d", in.R,in.G, in.B);
      @(posedge clk); //after 1 clock output will be obtained
      $display("Y = %d Cb = %d Cr = %d", out.Y, out.Cb, out.Cr);
    end
    $finish();
  end
  
  
endmodule : top

`endif

//probable filelist (filelist.f)


rgb_if.sv
ycbcr_if.sv
RGB_2_YCbCr.sv
ROM.sv


top.sv

+access+rw

// probable run script (run.sh)

vlib work
vlog -writetoplevels questa.tops -timescale 1ps/1fs -f filelist.f 
vsim -f questa.tops -c -do "vsim -voptargs=+acc=npr; run -all; exit" -voptargs=+acc=npr | tee log

References

[1] Keith Jack. Video demystified: a handbook for the digital engineer. Elsevier, 2011